Werkplan Wiswijs over de niveau 4 opleiding
Leerjaar 1 (ongeveer 1/2 jaar) Wiskunde A (blok 1 en bijlage D) (15 werkbare uren incl toetsing en herkansing)Leerjaar 1 en 2 (ongeveer 1 1/2 jaar) Wiskunde B (blok 2 en 3 bijlage 4A) + Project. (40 werkbare uren incl toetsing en herkansing, project 5 werkbare uren in samenwerking met vakafdeling)
Leerjaar 3 en 4 (resp 1 en 2 contacturen) Wiskunde C1 (overige bijlagen) (90 werkbare uren incl toetsing en herkansing)
Wiskunde A
afhankelijk van het instapniveau kunnen onderdelen direct getoetst en afgetekend worden.
Blok 1helemaal.
Percentages en verhoudingen.
Omtrek, oppervlakte en inhoudberekening.
ruimtelijke figuren en hun oppervlakte en inhoud
prisma's cylinders
oppervlakte grondvlak * hoogte = volume
Kegels en piramides
oppervlakte grondvlak * hoogte = volume
3
Bol
![]()
![]() Cirkels
Cirkels
Bij cirkels speelt het getal Π een grote rol.
p is de verhouding tussen de omtrek en de doorsnee van een cirkel.
bij hoofdrekenen en schatten kan je ervan uitgaan dat Π gelijk is aan 3
De omtrek van een cirkel is dus Π maal de doorsnee (diameter)
en de diameter is tweemaal zo lang als de straal (radius)
De oppervlakte van een cirkel is ongeveer 3/4 van de oppervlakte van het vierkant dat er precies omheen past of 3 maal een vierkant wat een maat heeft van straal keer straal. (3 bij cirkels blijkt vaak Π te zijn)

Er zijn twee formules in omloop die beiden hetzelfde resultaat opleveren
![]()
![]()
Hierin is A de oppervlakte r de straal en D de diameter
Tekenen op Schaal.
Metriek stelsel.
Wetenschappelijk notatie.
Rekenmachine Bijlage D
Blok 2 hst 5functies en grafieken.
Statistiek weergeven van gegevens in tabellen en diagrammen (Excel)
Centrale waarden:
Rekenkundig Gemiddelde - Alle waarden bij elkaar opgeteld delen door het aantal waarden
Gewogen gemiddelde - Alle waarden met hun wegingsfactor vermenigvuldigd bij elkaar optellen en delen door de som van de wegingen.
Modus - Meest voorkomende waarde
Mediaan - Middelste waarden na sorteren
Wiskunde B
Blok 2
Hst 4 het oplossen van vergelijkingen met 1 en 2 onbekenden.
Hst 7.3 merkwaardige producten
Hst 6 Eerstegraads functies
Lineaire ongelijkheden.
Optimaliseren en kostprijsberekening als toepassing van lineaire vergelijkingen / ongelijkheden.
Blok 3
Hst 8 Tweedegraads vergelijkingen (zonder 8.4 ontbinden)
Hst 9 Analyse tweedegraads functies.
Hst bijzondere functies
Bijlage A4 Exponentiele groei als toepassing van exponentiele functies in economie en biologie. (oplossen, herkennen, tekenen en aflezen)
Wortelfuncties op zich, gelimiteerde processen (herkennen, tekenen en aflezen)
Derdegraads functiesop zich (relatie oppervlakte inhoud) (herkennen, tekenen en aflezen)
Gebroken functies (samenwerken / tegenwerken en parallelschakelingen) (herkennen, tekenen en aflezen)
Sinusfuncties (cyclische processen en hun functies) (herkennen, tekenen en aflezen).
Hst Meetkunde
Radialen als hoekmaat.
Goniometrie: sinus- en cosinusregel, SOS, CAS, TOA. (Total Station)
PoolcoŲrdinaten als plaatsbepaling.
Verweking (goniometrische) landmeet gegevens in Excel en/of Vectorworks
Hst statistiek
Statistiek, normale verdeling, e-norm.
Statistiek, verweking meetgegevens of waarnemingen in Excel
Project
Wiskunde C1
Bijlage B Analyse, differentieren
Foutanalyse.
Kansrekening.
Steekproeven.
Significantie van cijfers.
Wetenschappelijk notatie.
Correlatie en regressie.
Co-relatie is samenhang.
Gemeten waarden kunnen een bepaalde samenhang hebben. Als gemeten waarden heel dicht bij een beschreven lijn liggen (lijn of kromme) spreken we van een correlatie.
We beschrijven de lijn en geven aan hoe ver de gemeten waarden ervan afliggen.
Liggen alle waarden vrijwel op de lijn dan is er een correlatie van 1
is de lijn stijgend dan +1 is de lijn dalend dan -1
Naarmate de waarden verder van de lijn liggen wordt de correlatie kleiner.
Als de waarden helemaal geen structuur hebben is de correlatie 0
Je moet kunnen aangeven of een correlatie aanwezig is en in welke richting die gaat.
Of een correlatie geschat wordt op 0,4 of 0,6 is iets wat ik niet beoordeel.
Computerprogramma's kunnen dat precies uitrekenen, of je kan van elk punt op de lijn berekenen hoeveel SD het van de lijn verwijderd ligt, maar dat valt buiten de stof.
Correlatie. (Excel)
Regressie, inter- en extrapoleren (Excel)
Gebroken functies. (analyse)
Goniometrische en cyclische processen en hun functies (analyse).
Korte inleiding natuurlijke logaritmen (met grondtal e)
Toepassing Excel
Toepassing grafische rekenmachine
4.3 Lineaire ongelijkheden.
Bij lineair ongelijkheden is het = teken vervangen door:
> (groter dan)
< (kleiner dan)
(groter of gelijk aan)
(kleiner of gelijk aan)
In principe los je deze ongelijkheden op door er eerst een gewone vergelijking van te maken (dat levert in een grafiek een lijn op) en achteraf te bepalen of:
Het gebied boven de lijn erbij hoort of het gebied onder de lijn erbij hoort.
Bovendien moet je bepalen of de lijn zelf deel uitmaakt van de grafiek of niet.
Dat kun je doen door een willekeurig punt boven of onder de lijn in te vullen in de ongelijkheid en te kijken of dit een ware bewering oplevert.
Bijvoorbeeld:
De ongelijkheid y > 2x+1 lossen we op voor y = 2x+1
 Het resultaat ziet er zo uit:
Het resultaat ziet er zo uit:
Door nu het punt (0,5) dat boven de lijn ligt in te vullen in de ongelijkheid krijgen we de bewering:
5 > 0x+1 en dat is waar (5 is inderdaad groter dan 1)
De lijn zelf maakt geen deel uit van de ongelijkheid (in dat geval had er y => 2x+1 moeten staan), maar we kunnen het ook uitproberen:
Door nu het punt (0,1) dat op de lijn ligt in te vullen in de ongelijkheid krijgen we de bewering:
1 > 0x+1 en dat is niet waar (1 is niet groter dan 1)
Als de lijn geen deel uitmaakt van de grafiek wordt die als een gebroken lijn weergegeven de oplossing van deze ongelijkheid ziet er dan als volgt uit:

Optimaliseren en kostprijsberekening
Het voorbeeld aan het begin van hoofdstuk 4 komt direct uit de praktijk.
Als kostenbewuste ondernemer moet je telkens opnieuw vaststellen wat de voordeligste oplossing is.
Je kunt natuurlijk best een scheepslading voer kopen, maar als het bederft en je moet het weggooien heb je er niets aan.
Opslag kost ook geld, zeker als je niet teveel ruimte hebt of opslagmogelijkheden moet bouwen of kopen.
De vraag of iets kan renderen kan buitengewoon complex worden.
Wij gaan uit van redelijk overzichtelijke situaties.
Voorbeeld:
Een voerleverancier geeft korting naarmate er meer zakken voer tegelijk worden afgenomen.
10 zakken volle prijs Ä 150 (Ä 15,00 per zak)
100 zakken Ä 1.000 (Ä 10,00 per zak)
1000 zakken Ä 7.500 (Ä 7,50 per zak)
We gebruiken 10 zakken per maand.
De opslag kost aan ruimte Ä 1 per maand per 5 zakken
(Om aan te geven dat de werkelijkheid nog lastiger is zou je ervan uit kunnen gaan dat je geld moet lenen tegen een bepaalde rente om veel zakken tegelijk te kopen)
In het eerste geval liggen er gemiddeld 5 zakken per maand opgeslagen de kosten zijn dus Ä 5 per maand. + het voer Ä 150 = Ä 155 per maand
In 100 maanden is dat dus Ä 15.500,00
In het tweede geval liggen er gemiddeld 50 zakken over een periode van 10 maanden opgeslagen de kosten zijn dus Ä 50 per maand.
In 100 maanden is dat Ä 500 + het voer Ä 10.000 = Ä 10.500,00
In het laatste geval liggen er gemiddeld 500 zakken over een periode van 100 maanden opgeslagen de kosten zijn dus Ä 100 per maand.
In 100 maanden is dat Ä 10.000 + het voer Ä 7.500 = Ä 17.500,00
In het eerste geval zijn de kosten per zak Ä 16,00
In het tweede geval zijn de kosten per zak Ä 10,50
In het laatste geval zijn de kosten per zak Ä 17,50
De tweede regeling is dus voor ons bedrijf het voordeligst.
Zou dit niet makkelijker kunnen met een grafiek?
Jazeker, maar dan moet de ontwikkeling van de kosten een stelsel van rechte lijnen zijn.
(het kan ook wel voor andere grafieken, maar dan moet je meestal integreren)
Bij voorbeeld om uit te rekenen welk mobieltje je moet kopen bij een bepaald aantal belminuten.
Mobieltje 1 prepay belkosten Ä 0,10/ minuut
Mobieltje 2 abonnement Ä 10 per maand eerste 90 minuten gratis bellen, belkosten Ä 0,02 per minuut
We maken een grafiek met als x-as het aantal minuten
En als y-as de kosten.
De eerste is makkelijk y = 0.1x
De tweede valt uiteen in twee stukken van het domein
Voor x = [0..90] geldt y = 10
Daarna geldt y = 0.02(x-90)+10
We gaan op zoek naar snijpunten, in het eerste stuk [0..90]
y2 = 10 en bij de andere geldt y1 = 0.1x
Vullen we y = >10 in dan vinden we voor x een waarde van 100 en dat valt buiten het domein. In de eerste 90 minuten is er geen snijpunt!
We gaan verder:
In het tweede deel geldt voor het snijpunt 0.1x = 0.02(x-90)+10
Haakjes wegwerken levert 0.1x = 0.02x + 8.2
Beide zijden† 0.02x aftrekken = 0.08x = 8.2
Beide zijden delen door 0.08 levert 102.5 het snijpunt ligt dus bij 102.5 minuten en een prijs van (vul in in ťťn van de vergelijkingen) Ä 10.25
Boven dit aantal minuten is een abonnement in dit voorbeeld goedkoper dan prepayed
 Uitgetekend ziet het er als volgt uit:
Uitgetekend ziet het er als volgt uit:
Voorbeelden en sommen uit het hoofdstuk optimaliseren van toepassen wiskunde toevoegen
Bijzondere functies
ExponentiŽle functies
Bijlage A4 Exponentiele groei als toepassing van exponentiele functies in economie en biologie. (oplossen, herkennen, tekenen en aflezen)
Functies met de volgende algemene gedaante;†
y(t) = y(b)∑at
worden exponentiele functies genoemd. Omdat de variabele (t) als exponent gebruikt wordt.
Deze klasse van functies beschrijven groeiprocessen (of afbraak).
Ze hebben de neiging om steeds sneller te gaan stijgen (of steeds langzamer te gaan dalen)
Voorbeelden zijn de ongeremde groei van bacterien, de groei van spaargeld bij een samengestelde intrest (rente over rente).
Maar ook radioactief verval en verdunningen van stoffen, reactiesnelheden en energieoverdracht worden hiermee beschreven.
Wat betekenen de onderdelen van de algemene formule;
y(t) is de hoeveelheid op een zeker tijdstip t
y(b) is de hoeveelheid aan het begin van de grafiek
a is de groeifactor
t is de tijd die is verlopen sinds b (aantal stapjes)
a de groeifactor kun je uitrekenen door te bepalen waarmee je moet vermenigvuldigen om 1 stapje t verder te komen.
We gaan wat sparen en brengen Ä 20 naar een bank die een rente van 4 % per jaar geeft. Na 1 jaar kijken we op de rekening en we hebben Ä 20.08, niet spectaculair maar er is groei, en het is wel 1.04 keer zoveel geworden, de groeifactor is dus 1.04 met deze gegevens kunnen we verder rekenen, we vullen ze in in de algemene formule.
Ä(t) = 20∑1.04jaren
Als we een tabelletje maken over een periode van 50 jaar en daar een grafiek van tekenen dan zien we het volgende:

0† 20,00
1† 20,80
2† 21,63
3† 22,50
4† 23,40
5† 24,33
6† 25,31
7† 26,32
8† 27,37
9† 28,47
10†††††††††††††††† 29,60
11†††††††††††††††† 30,79
12†††††††††††††††† 32,02
13†††††††††††††††† 33,30
14†††††††††††††††† 34,63
15†††††††††††††††† 36,02
16†††††††††††††††† 37,46
17†††††††††††††††† 38,96
18†††††††††††††††† 40,52
19†††††††††††††††† 42,14
20†††††††††††††††† 43,82
21†††††††††††††††† 45,58
22†††††††††††††††† 47,40
23†††††††††††††††† 49,29
24†††††††††††††††† 51,27
25†††††††††††††††† 53,32
26†††††††††††††††† 55,45
27†††††††††††††††† 57,67
28†††††††††††††††† 59,97
29†††††††††††††††† 62,37
30†††††††††††††††† 64,87
31†††††††††††††††† 67,46
32†††††††††††††††† 70,16
33†††††††††††††††† 72,97
34†††††††††††††††† 75,89
35†††††††††††††††† 78,92
36†††††††††††††††† 82,08
37†††††††††††††††† 85,36
38†††††††††††††††† 88,78
39†††††††††††††††† 92,33
40†††††††††††††††† 96,02
41†††††††††††††††† 99,86
42†††††††††††††††† 103,86
43†††††††††††††††† 108,01
44†††††††††††††††† 112,33
45†††††††††††††††† 116,82
46†††††††††††††††† 121,50
47†††††††††††††††† 126,36
48†††††††††††††††† 131,41
49†††††††††††††††† 136,67
50†††††††††††††††† 142,13
Niet alleen hebben we
na 50 jaar zomaar Ä 142.13 op de bank maar ook zie
je dat de groei steeds sneller gaat.
Een ander voorbeeld
is de afname van ziekteverwekkers door het gebruik van antibiotica hier krijgen
we te maken met een groeifactor kleiner dan 1 (maar groter dan 0)
Probeer zelf eens met
de volgende gegevens een grafiek te maken over een periode van een etmaal.
De groeifactor is
0.75 per uur aan het begin zijn er 1.000.000 bacteriŽn.
Uitwerking:
Y(t)
= 1000000∑0.75t
Voorbeelden en sommen uit toepassen wiskunde en de
praktijk
Het is handig om bij
het uitwerken van vraagstukken even een aantekening te maken in wat voor
stapjes t loopt.
Exponentiele functies
hebben als kenmerk dat ze niet bij 0 kunnen beginnen of eindigen. (dit wordt asymptotisch gedrag genoemd)
Bij groei is het duidelijk als je met niets begint wordt het ook nooit wat.
Omgekeerd is het bij
afbraak minder voor de hand liggend, toch is het soms letterlijk van levensbelang,
bijvoorbeeld bij het gebruik van antibiotica, het is vrijwel uitgesloten dat je
met een kuur alle bacteriŽn doodt. Maar je moet wel proberen om zoveel mogelijk
te bereiken. (Dieren)artsen schrijven kuren voor die afgemaakt moeten worden
omdat dan het aantal overlevende bacteriŽn zo klein is dat er weinig gevaar
optreed voor resistentie.
Als er te veel
overlevende bacteriŽn zijn kunnen die een populatie voortbrengen die heel goed
tegen antibiotica kan.
Kuren afmaken
betekent dat je nog moet doorgaan met pillen en drankjes nadat je je al weer
veel beter voelt.
Een bijzonder
probleem doet zich voor als je de vraag stelt; Hoe lang duurt het totÖ.?
Dan moet je de
exponent uitrekenen (de rest is dan bekend)
Daarvoor is een
manier die je hier als kunstje geleerd krijgt, gewoon doen en verder niet
nadenken.
Er is een wiskundige
bewerking die van machten vermenigvuldigingen maakt
Van wortels delingen
van delingen aftrekkingen van vermenigvuldigingen
optellingen. Gelukkig kan je rekenmachine dat kunstje ook (gelukkig want
rekenmachines kunnen alleen maar optellen en aftrekken en dit kunstje, het
schuiven met bitjes)
Het kunstje heet de
logaritme nemen.
Stel je wilt weten
hoe lang het duurt bij een rente van 8 % per jaar om van een inleg van Ä 100 Ä 1.000.000 te
maken.
Dat kun je als volgt
uitrekenen;
Vul wat je weet in in
de algemene formule:
1.000.000 = 100∑1.08t(t
in jaren)
Beide zijden delen
door 100 levert:
10.000 = 1.08t
Door nu aan beide
zijden de logaritme te nemen krijg je:
log(10.000) = log(1.08) ∑ t
Beide zijden delen
door log(1.08) geeft t
Je kunt de logaritmen
uitrekenen
log(10.000) = 5 en log(1.08) = 0.033423755
maar dat hoeft niet op je rekenmachine kan je het volgende doen;
10000 log / 1.08 log = 119.68 jaar
CEM heeft een
incubatietijd van 2 dagen
de besmetting begint met 1 bacterie
De groeifactor is
1,315 per uur
Geef de
algemene formule voor dit exponentiele verband
Maak een tabel
van het verloop per 3 uur
Teken de
grafiek.
Hoeveel
bacteriŽn zijn er
na die 2 dagen?
Mok kan als het niet
behandeld wordt leiden tot bloedvergiftiging
de besmetting begint met 1 bacterie
bij 1000000 bacteriŽn treed bloedvergiftiging op
de groeifactor is 2, de tijdseenheid is 1 dag
Geef de
algemene formule voor dit exponentiele verband
Maak een tabel
van het verloop per dag
Teken de
grafiek.
Na hoeveel
dagen treed bloedvergiftiging op?
We behandelen met
antibiotica en starten de behandeling 14 dagen na de besmetting
de groeifactor is 0.157, de tijdseenheid is 1 dag
Met hoeveel
bacteriŽn beginnen we?
Maak een tabel
van het verloop per dag
Teken de
grafiek.
Na hoeveel
dagen is het aantal bacteriŽn onder de 10 gedaald?
Droes is een
bacteriŽle infectie.
In een weefselmonster
meten we 2 dagen na de infectie 20 bacteriŽn per mm3
De groeifactor van
Droes-bacteriŽn is 2.
De eenheid van tijd
is 6 uur. Als de telling boven de 10.000 bacteriŽn per mm3 komt
wordt het paard zichtbaar ziek.
Schrijf de
algemene formule voor dit exponentiŽle verband op.
Bereken wat de
incubatietijd van droes is (de tijd tussen de besmetting en de eerste
ziekteverschijnselen).
De ziekte is op zijn
hoogtepunt als de telling 200.000 bacteriŽn per mm3 is.
Bereken na
hoeveel dagen deze telling bereikt wordt.
Op het hoogtepunt van
de ziekte neemt het immuunsysteem van het paard de overhand. De groeifactor is
nu 0,25 geworden.
Schrijf de
algemene formule voor dit exponentiŽle verband op.
Bereken na
hoeveel dagen de telling weer onder de 20 bacteriŽn per mm3 komt.
d. Teken het
grafiek waarin het aantal bacteriŽn is uitgezet tegen de dagen.
2
2
20
3
3
160
4
4
320
5
5
640
6
6
1280
7
7
2560
8
8
5120
8,965784
8,965784
10000
9
9
10240
10
10
20480
11
11
40960
12
12
81920
13
13
163840
13,28771
13,28771
200000
14
1
50000
15
2
12500
16
3
3125
17
4
781,25
18
5
195,3125
19
6
48,82813
6,643856
6,643856
20
20
7
12,20703
Een bijzondere klasse
van exponentiele functies zijn de functies met als exponent een getal kleiner
dan 1 (maar groter dan 0) bij voorbeeld 0.5 deze heet
wortelfunctie (want x0.5 =
Vx)
Wortelfuncties zijn
kenmerkend voor gelimiteerde processen.
In de natuur zie je
dat groei beperkt wordt door de hoeveelheid voedsel, economische groei wordt
beperkt door de hoeveelheid grondstoffen etc.
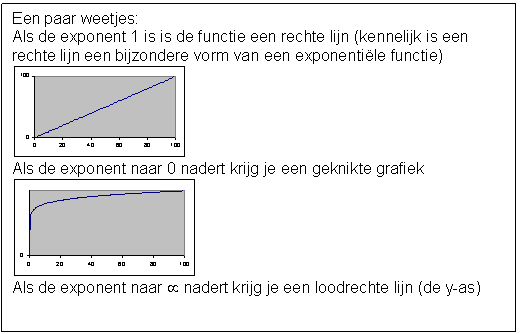
Als de exponent 1
is is de functie een rechte lijn (kennelijk is een rechte lijn een
bijzondere vorm van een exponentiŽle functie)
Als de exponent
naar 0 nadert krijg je een geknikte grafiek
Als de exponent
naar Ķ nadert krijg je een loodrechte
lijn (de y-as)
Derdegraads functies
(relatie oppervlakte
inhoud) (herkennen, tekenen en aflezen)
Je hebt al kennis
gemaakt met tweedegraads functies de grafieken hiervan zijn de zogenaamde
parabolen Tweede machten zijn of allemaal positief of allemaal negatief, een
parabool kan dus naar oneindig + of naar oneindig - lopen maar niet beide.
Er zitten juweeltjes bij:
y = ax3 + bx2 + cx + d
maar wij beperken ons hier tot y = x3
dus met a = 1 en b,c,d = 0
In de praktijk
gebruiken we toch voornamelijk het positieve deel van de† functie. Van de dingen die met een
derde macht toenemen is volume wel de bekendste, je kunt bijvoorbeeld het
volume van een kubus, bol of cilinder schrijven als functie van de diameter of
hoogte.
Op die manier kun je
de optimale verhoudingen uitrekenen tussen materiaalgebruik en volume. Je kunt
ook de relatie tussen oppervlakte (een tweedegraads functie) en volume gaan
bekijken.
Zo kun je uitrekenen
dat het in koude gebieden (op de polen) gunstig is om dik (rond) en groot te
zijn en verklaren waarom in dit klimaat alleen dikke ronde en grote dieren
voorkomen. Die combineren de voordelen van een groot volume met een relatief
kleine buitenkant en koelen dus minder af.
Een paling is een
cilinder van
Een muis is een
cilinder van
Een cavia is een
kegel van
Een ijsbeer is een
bol met een diameter van
(samenwerken /
tegenwerken en parallelschakelingen) (herkennen, tekenen en aflezen)
Functies met de
algemene gedaante;
Worden gebroken
functies genoemd
dus met b = 1 en a,c,d = 0
Je ziet direct dat er
een aantal onmogelijkheden in deze functie zitten, Als x = 0 gaat het mis want
delen door nul geeft een onbepaalde utkomst.
Ook is er geen deling
denkbaar die 0 als uitkomst heeft.
Deze functie is dus
onoplosbaar voor x = 0 en voor y = 0
Deze functies
beschrijven het effect van samenwerking. Maar gen ook de grenzen aan (als negen
vrouwen samenwerken kunnen ze niet in 1 maand een kind
krijgen)
Als twee mensen met
een zelfde werk tempo samenwerken is de klus in de helft van de tijd gedaan dat
is duidelijk.
Maar als iemand 20
hokken per uur kan schoonmaken en hij gaat samenwerken met een stagiere die
maar 10 hokken per uur kan schoonmaken kan je uitrekenen hoe lang het duurt
door de volgende berekening:
20 hokken per uur is
1 hok per 3 minuten
samen met 1 hok per 6 minuten
De grenzen worden
bereikt op een moment dat de mensen elkaar in de weg gaan lopen.
(cyclische processen
en hun functies) (herkennen, tekenen en aflezen).
y = a - b sin(cx-d)
De functie y = sin(x)
(x in graden)
Uit het feit dat voor
x een hoekmaat gebruikt wordt kun je al bedenken dat er iets aan het draaien
is.
Het is een zij
aanzicht van een spiraal Het is een manier om naar kringlopen te kijken.
De stand van de zon,
de loop van de seizoenen, maar ook allerlei processen zoals de hormoonspiegel
in het bloed, en daarmee de (be)vruchtbaarheid.
De
vruchtbaarheidcyclus van een merrie kan je schrijven als:
y=10*sin(2*Π/22*x)
hierbij is y de vruchtbaarheids-hormoonspiegel en x het aantal
dagen.
als y > 9,5 dan vruchtbaar
Wanneer begint dat,
hoe lang duurt dat?
sin(2*Π/22*x) moet dan groter zijn dan 0,95,
dat gebeurt bij hoeken van groter dan 71.8į en kleiner
dan 108.2į of tussen 1,25 rad en 1,89 rad
vul dat in dan vind je:
1.253 = 2Π/22*x
22*1.253/2Π = x = 4.39
1.888 = 2*Π/22*x
22*1.888/2Π = x = 6.61
dat is van dag 4, half 10 's morgens tot dag 6, 10 over half 3 's middags
2.22 dagen oftewel 2 dagen en 5 uur en een kwartier
Hst Meetkunde
Radialen als hoekmaat.
Er zijn veel
gelijkwaardige manieren om een hoek aan te geven, we zijn gewend aan graden
waarbij een cirkel 360 graden (deg) beslaat.
Je zou een hoek ook
in uren kunnen verdelen zodat een cirkel uit 12 uren bestaat. (gevaar op 9 uur)
Of een tandwiel met 40
tanden heeft een omtrek van 40 tanden en die kun je dus ook als hoekmaat
gebruiken.
Cirkels hebben een
omtrek die ook een hele cirkel is, de omtrek van een cirkel is 2Πr dus 2Πr is ook een goede maat voor een hele cirkel.
Deze laatste hoekmaat
wordt bijvoorbeeld door Excel gebruikt.
Ook rekenmachines
hebben de mogelijkheid om ermee te werken.
Als een hoek wordt
uitgedrukt in stukjes van de cirkelomtrek noemen we dit radialen (rad)
1 rad is dus gelijk
aan 360/2Π
= 57.296 graden
1 graad is dus 2Π/360 = 0.017 radialen
Rekenmachine in de
DEG (degree = graden) modus
Rekenmachine in
de RAD (radialen) modus
Van hoek naar
sinus gebruik de sin functie van de rekenmachine
Van sinus naar
hoek gebruik de sin-1 functie van de rekenmachine (shift sin)
Goniometrie: sinus- en cosinusregel, SOS, CAS, TOA. (Total Station)
Met een paar simpele
regels is het mogelijk om van een driehoek waarvan 3 dingen bekend zijn alle
andere onderdelen precies te berekenen.
We spreken af:
Hoek α ligt tegenover zijde A
Hoek β ligt tegenover zijde B
Hoek γ ligt tegenover zijde C
Bij rechthoekige
driehoeken
De schuine zijde van
een rechthoek ligt tegenover de rechte hoek en is het langste.
Aanliggend betekent
aan de hoek vast waarmee we rekenen.
Overstaand betekent
tegenover de hoek waarmee we rekenen.
Regel 1 de
binnenhoeken van een driehoek (op een vlak)
zijn samen 180 graden
Regel 2 sinusregel
Regel 3 cosinusregel
In rechthoekige
driehoeken geldt:
Regel 3a pythagoras
Regel 4 de verhouding
overstaande / schuine =
sin (hoek)
Regel 5 de verhouding
aanliggende / schuine = cos(hoek)
Regel 6 de verhouding
overstaande / aanliggend = tan(hoek)
Regel 7 De
oppervlakte van een driehoek is altijd de helft van de rechthoek die er precies
omheen past, oftewel
2 De sinusregel zegt:
3 De cosinusregel
zegt:
Werkt als een pincet
als de hoek kleiner wordt dan knijpen de punten bij elkaar.
Of
3a Pythagoras is een
bijzonder geval van de cosinusregel als hoek γ
90 graden wordt is de cosinus 0 en vervalt de gele term -2ABcos(γ)
Die zegt in wezen dat
de oppervlakte van het vierkant bij A en de oppervlakte van het vierkant bij B
samen even groot zijn als de oppervlakte van het vierkant bij C.
4
de verhouding overstaande / schuine† = sin (a)
5 de verhouding
aanliggende / schuine = cos(a)
PoolcoŲrdinaten als plaatsbepaling.
Om ergens te komen
kun je via een rechthoekig assenstelsel aangeven hoeveel je in de x richting
moet en hoeveel in de y richting.
In het dagelijks leven gebruiken we ook vaak wijzen in een richting
en aangeven hoe ver je moet gaan. Deze laatste manier os ook mogelijk in een rechthoekig
coordiantenstelsel waarbij de afspraak is gemaakt dat de positieve x as als 0
geldt en er linksom geteld wordt.
De aarde zelf is
ingedeeld met dubbele poolcoordinaten. Je kunt je voorstellen dat er een
mannetje in het midden van de aarde zit met zijn neus naar de evenaar ter
plaatse van het snijpunt met de 0-meridiaan
(ruwweg
Vanaf die plaats
wijst hij dingen aan
Bijvoorbeeld
Amsterdam 52.25 noord 4.40 oost
Of Zwolle 52.30 noord
6.15 oost
Melbourne AustraliŽ
40.00 zuid 125 oost
Deze posities worden
gebruikt op (zee)kaarten en door het GPS satellietnavigatie systeem.
Een en ander is
genormaliseerd in het WGS 84 (World Geodetic System 1984)
Dit systeem heeft
grote voordelen en maar 1 nadeel in de noord-zuid richting komt een graad
overeen met 60 zeemijl (NM, 1 NM =
In de
oost-west richting komen de graden steeds dichter bij elkaar, bij de
pool liggen alle 360 graden op ťťn punt.
Een minuut in de oost-west richting is cos(breedte)*1852 meter
In Zwolle is een
minuut naar het oosten
Als je met kaarten of
met GPS werkt krijg je hiermee te maken.
Rijkswaterstaat
gebruikt voor Nederland op zijn kaarten ook nog een X-Y net de zogenaamde
Amersfoortse coŲrdinaten (omdat de oorsprong van het coŲrdinatenstelsel daar
ligt
Verweking
(goniometrische) landmeet gegevens in Excel en/of Vectorworks
Hst statistiek
Statistiek, normale
verdeling, e-norm.
Relatieve
frequentie
Om
groepen van ongelijke grootte met elkaar te kunnen vergelijken moet je ze
zodanig normaliseren dat de groepen een gelijke basis hebben bijvoorbeeld doe
alsof elke groep uit honderd waarden bestaat. (dat is precies wat procenten
betekenen)
zoveel
van het geheel
Spreiding
Er
blijkt een hele grote groep van verdelingen te zijn
die dezelfde structuur hebben.
De
normale verdelingen
De
eigenschappen van de normale verdeling zijn goed beschreven, zo goed dat je
door twee waarden aan te geven de gehele grafiek kan bepalen.
De
eerste waarde die je moet weten is het rekenkundig
gemiddelde,
De
klok-vormige kromme (curve) die hoort bij normale verdelingen heet de Gauss
kromme.
In
het midden zit het gemiddelde en links en rechts van het gemiddelde zitten
evenveel waarden.
Hoe
verder je bij het gemiddelde vandaan komt (naar boven of beneden) hoe zeldzamer
de waarden worden.
Je
hebt hele steile krommen, een kleine spreiding of hele
vlakke met een grote spreiding.
Bij
normale verdelingen kan je de spreiding uitdrukken in een eenheid die Standaard
deviatie wordt genoemd.
Er
is een genormaliseerde manier bedacht om die standaarddeviatie uit te rekenen.
Bekijk
het is in het boek en onthoud hoe je het op de rekenmachine kunt uitrekenen.
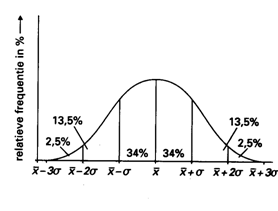
De
normale verdeling speelt zich vrijwel geheel af tussen het gemiddelde en 3
standaarddeviaties meer of minder.
Je
kunt dus een standaard grafiek tekenen met de Gauss kromme en daaronder de x-as
die je verdeelt in 6 stukjes met in het midden de gemiddelde waarde. de maatverdeling is de standaarddeviatie.
Je
ziet dat je voor grote spreidingen een grote standaarddeviatie nodig hebt en
voor kleine spreidingen een kleine standaarddeviatie.
De
oppervlakte van de grafiek is alle waarden dus 100%
Nu
blijkt dat bij normale verdelingen bij bepaalde stukjes vaste oppervlaktes
horen (blz 59)
Bij
het vullen van zakken en potten worden machines ingesteld op een bepaalde
waarde. De resultaten zullen bij nawegen een normale verdeling vertonen.
Als
je de machine instelt op de waarde die op de verpakking staat dan krijgt de
helft van de klanten te weinig en de andere helft te veel.
Consumenten
vinden dit onacceptabel.
Er
is afgesproken om machines zodanig in te stellen dat niet meer dan 2,5% van de
klanten minder krijgt dan de aangegeven hoeveelheid.
Dit
is vastgelegd in de e-norm.
Je
begrijpt dat de standaarddeviatie samenhangt met de nauwkeurigheid van de
machine, je gaat geen machine die is gemaakt voor medicijnen gebruiken om
voerbrok af te wegen.
Z-waarde
Als
je bedenkt dat de x-as is verdeeld in standaarddeviaties, dan kan je wel nagaan
dat de niet op gehele waarden hoeft uit te komen.
Ook
tussenliggende waarden zijn mogelijk.
De
oppervlakte onder een grafiek bepaal je door te integreren, dat is lastig maar
wel te doen. Het resultaat hiervan is een tabel, die aangeeft wat de
oppervlakte van een grafiek is tot een bepaald punt. Integreren begint altijd
links in het domein, zodat je soms waarden van elkaar moet aftrekken om de
gevraagde waarden te vinden.
Statistiek, verweking
meetgegevens of waarnemingen in Excel
Project

eenheid t
6 uur
Wortelfuncties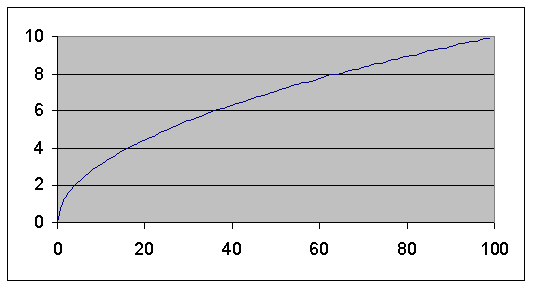
Derdegraads functies kunnen dat wel.

 De algemene
vergelijking van een derdegraads functie is
De algemene
vergelijking van een derdegraads functie is
Gebroken functies
![]()
![]()
Wij beperken ons tot;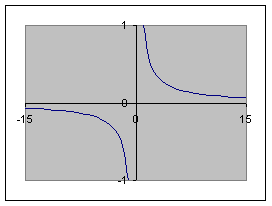
Niet alleen is de functie een breuk,
ook de grafiek is "gebroken"![]()
3 hokken per 6 minuten samen doen ze 20
hokken in 40 minuten
Sinusfuncties 
Ziet er als volgt
uit, 

![]()
in een bepaalde driehoek is de verhouding tussen een zijde en de sinus
van de tegenoverliggende hoek constant.![]()
![]()
![]()


6 de verhouding overstaande /
aanliggende = tan(a)
 We
moeten weten wat de modus en de mediaan is, in elk geval of die vrijwel
overeenkomen met het rekenkundig gemiddelde. Als dat
het geval is is er waarschijnlijk sprake van een normale verdeling.
We
moeten weten wat de modus en de mediaan is, in elk geval of die vrijwel
overeenkomen met het rekenkundig gemiddelde. Als dat
het geval is is er waarschijnlijk sprake van een normale verdeling.









